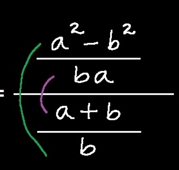Fracciones complejas algebraicas:
Una fracción compleja es aquella cuyo numerador o denominador ( o ambos ) esta conformado por otras fracciones.
Ejemplos:
Pasos para simplificar fracciones complejas:
- Resolver completamente las operaciones presentes en el numerador y denominador de la fracción compleja.
- Convertir una fracción compleja en una fracción simple.
3. Se simplifica al máximo la fracción algebraica resultante.
Aquí vamos a ver dos ejemplos de fracciones complejas:
1._
1. Lo primero que vamos hacer es ponerle un denominador al (1).
2. Aquí utilizamos el método de la carita feliz porque multiplicamos cruzados y los dos denominadores
.
3. Después que obtenemos el resultado con este método procedemos a multiplicar con el método de la oreja que es medios con medios y extremos con extremos
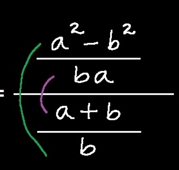
4. Después que tenemos la fracción de multiplicación del numerador y denominador que es esta etapa y la hacemos una fracción simple: como lo vamos aquí:
5. En este paso ya pasamos a simplificar los terminos iguales y nos queda así como es una diferencia de cuadrados perfectos.
6. Luego pasamos hacer este procedimiento que es la suma por la diferencia de cuadrados que es el resultado del numerador y en el denominador sigue igual el producto. como lo vemos aquí
7. Observamos que aquí hay factor común en el numerador y denominador, en lo cual pasamos a simplificar.
8. Bueno ya simplificado queda la respuesta planteada así.
2._ Este es el segundo ejemplo de fracción compleja:
*** Aquí va el numerador
1. Este es un ejercicio diferente al anterior ya que lo vamos a resolver por separado, primero resolvemos el numerador luego el denominador y cuando tengamos ambos resultados entonces construimos la fracción compleja, ya con una sola fracción arriba y abajo para convertirla en una fracción simple.
2. Comencemos con el numerador donde tenemos una suma de fracciones algebraicas heterogéneas, en el cual el MCD es el producto de los denominadores
3. Aquí procedemos a multiplicar con el método de la carita feliz que es en forma de (x).
4. Y sale esta respuesta ya multiplicada y luego pasamos desarrollar el numerador en el cual aplicamos la propiedad distributiva multiplicando lo de afuera con lo que esta dentro del paréntesis así y el denominador pasa con el mismo producto indicado:
6. En el siguiente paso ya aplicada la función distributiva queda otra respuesta como lo vemos a continuación así:
7. En este paso, pasamos a reducir terminos semejante como lo mostramos con las flechas de colores, y aquí va la respuesta de la reducción de terminos y ademas es el resultado del numerador.
*** Ahora pasamos al denominador
1. Aquí tenemos una resta de fracciones algebraicas
2. El (MCD) es el producto de estas dos expresiones del denominador que son: (x-2)(x+6) : y lo pasamos a realizar con el método de la carita feliz así:
3. Y aquí ya tenemos ensamblada la operación de la carita feliz: 4. Y así mismo aplicamos la propiedad distributiva como lo mostramos con las flechas de colores y el denominador pasa con el producto indicado:
4. Ahora vamos hacer la reducción de terminos semejantes en el numerador y lo mostramos con los colores en el numerador y queda la operación así:
5. Y esta es la respuesta del denominador. Luego todo pasa así desde el comienzo ya con el numerador y denominador ya resueltos para pasar hacer la fracción así:
*** Esta es la fracción con los resultados del numerador y del denominador con una sola fracción arriba y abajo:
6. Cambiamos esto en una fracción simple simplificando el numerador con el denominador ya que son iguales y el orden de los factores no alteran el producto:
7. Y nos queda así esta es la respuesta del ejercicio, en el numerador y en el denominador, esto no es posible simplificar a pesar que en el numerador podemos extraer el factor común de 8 pero eso no hace que se simplifique la fracción y termina así.
