Definición formal de límite
Funciones de variable real
Si la función tiene límite en podemos decir de manera informal que la función tiende hacia el límite cerca de si se puede hacer que esté tan cerca como queramos de haciendo que esté suficientemente cerca de siendo distinto de .
Los conceptos cerca y suficientemente cerca son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice:
El límite de una función f(x), cuando x tiende a c es L si y sólo si para todo , existe un tal que para todo número real x en el dominio de la función, si entonces .
Esto, escrito en notación formal:
- En la siguiente gráfica se observa claramente, los acercamientos de un x a c y de un f(x) al límite L.
INTRODUCCION
Las funciones matemáticas, en términos simples, corresponden al proceso lógico común que
se expresa como “depende de”. Este proceso lógico se aplica a todo lo que tiene relación a un
resultado o efecto sea este medible o no en forma cuantitativa.Las funciones matemáticas pueden referirse a situaciones cotidianas:
Ejempo1.
el agua que consumimos, a cada metro cúbico consumido le corresponde un valor
determinado.
Ejemplo2. La sombra proyectada por un edificio que depende de lala estatura de un niño que depende de su edad.Ejemplo 3. el costo de una llamada telefónica que depende de su duración;
Ejemplo 4. el costo de enviar una encomienda que depende de su peso;Los números de la derecha son los cuadrados de los de la izquierda.A modo de ejemplo, ¿cuál sería la regla que relaciona los números de la derecha con los de la izquierda en la siguiente lista?: 1 --------> 1 2 --------> 4 3 --------> 9 4 --------> 16x -------> x2.La regla es entonces "elevar al cuadrado":Para referirse a esta regla podemos usar un nombre, que por lo generales la letra f (de función). f es la regla "elevar al cuadrado el número".Usualmente se emplean dos notaciones:x --------> x2 ó f(x) = x2 .Así, f(3) significa aplicar la regla f a 3. Al hacerlo resulta 32 = 9.Entonces f(3) = 9. De igual modo f(2) = 4, f(4) = 16 f(a) = a2, etc.
Definición formal:
Una función f es una regla que asigna a cada elemento x de un conjunto X exactamente un elemento, llamado f(x) de un conjunto Y. Otra definición equivalente es: sean X e Y dos conjuntos. Una función de X en Yen X.
observa con atención el siguiente video. Aquí aclaras la diferencia entre relación y función
Se dice que el dominio de una función son todos los valores que puede tomar el conjunto del dominio y que encuentra correspondencia en el conjunto llamado codominio, generalmente cuando se habla del plano, el dominio es el intervalo de valores que están sobre el eje de las X´s y que nos generan una asociación en el eje de las Y´s.
El otro conjunto que interviene en la definición es el conjunto llamado codominio o rango de la función, en ocasiones llamado imagen, este conjunto es la gama de valores que puede tomar la función; en el caso del plano son todos los valores que puede tomar la función o valores en el eje de las Y´s.
También, cuando se grafica en el plano cartesiano se tiene una relación de dos variables, considerando como variable aquella literal que esta sujeta a los valores que puede tomar la otra.
Son aquellas variables que como su nombre lo indica, dependen del valor que toma las otras variables Por ejemplo: f(x)= x, y o f(x) es la variable dependiente ya que esta sujeta a los valores que se le subministre a x.
VARIABLE INDEPENDIENTE.
Es aquella variable que no depende de ninguna otra variable, en el ejemplo anterior la x es la variable independiente ya que la y es la que depende de los valores de x.
VARIABLE CONSTANTE.
Es aquella que no esta en función de ninguna variable y siempre tiene el mismo valor ejemplo:
Y=2, la constante gravitacional, entre otras.
observemos con los siguientes videos, sobre el dominio y rango de una función
RELACIONES MATEMÁTICAS
Una relación binaria es una relación entre dos conjuntos.
El concepto de relación implica la idea de enumeración, de algunos de los elementos, de los conjuntos que forman tuplas.
Un caso particular es cuando todos los conjuntos de la relación son iguales: en este caso se representa como , pudiéndose decir que la relación pertenece a A a la n.
En las relaciones se diferencian los tipos según el número de conjuntos en el producto cartesiano, que es el número de términos de la relación:
- Relación unaria: un solo conjunto
- Relación binaria: con dos conjuntos
- Relación ternaria: con tres conjuntos
- Relación cuaternaria: con cuatro conjuntos
- Relación n-aria: caso general con n conjuntos
Producto cartesiano
En matemáticas, el producto cartesiano de dos conjuntos es una operación, que resulta en otro conjunto, cuyos elementos son todos los pares ordenados que pueden formarse de forma que el primer elemento del par ordenado pertenezca al primer conjunto y el segundo elemento pertenezca al segundo conjunto.Por ejemplo, dados los conjuntos:ysu producto cartesiano es:El producto cartesiano recibe su nombre de René Descartes, cuya formulación de la geometría analítica dio origen a este concepto- DEFINICIÓN
- Un par ordenado es una colección de dos objetos distinguidos como primero y segundo, y se denota como (a, b), donde a es el «primer elemento» y b el «segundo elemento». Dados dos conjuntos A y B, su producto cartesiano es el conjunto de todos los pares ordenados que pueden formarse con estos dos conjuntos:El producto cartesiano de A y B es el conjunto A × B cuyos elementos son los pares ordenados (a, b), donde a es un elemento de A y b un elemento de B:
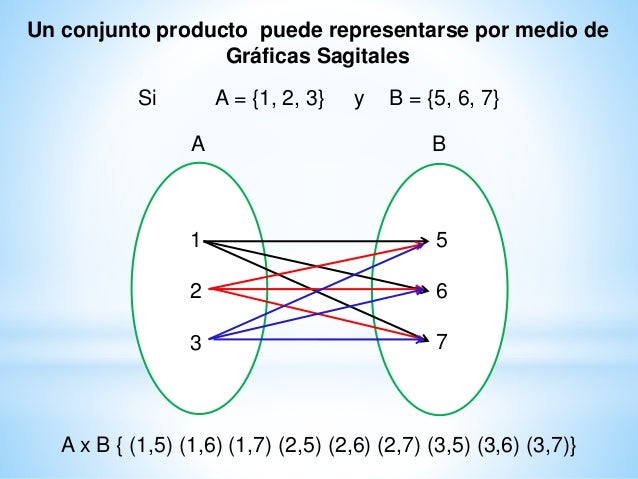
- El producto cartesiano se puede puede representar gráficamente de dos formas:
- 1. Plano cartesiano
- 2. Diagramas sagitales
observa el siguiente video
FUNCIONES
INTRODUCCION
Las funciones matemáticas, en términos simples, corresponden al proceso lógico común que
se expresa como “depende de”. Este proceso lógico se aplica a todo lo que tiene relación a un
resultado o efecto sea este medible o no en forma cuantitativa.Las funciones matemáticas pueden referirse a situaciones cotidianas:
Ejempo1.
el agua que consumimos, a cada metro cúbico consumido le corresponde un valor
determinado.
Ejemplo2. La sombra proyectada por un edificio que depende de lala estatura de un niño que depende de su edad.Ejemplo 3. el costo de una llamada telefónica que depende de su duración;
Ejemplo 4. el costo de enviar una encomienda que depende de su peso;Los números de la derecha son los cuadrados de los de la izquierda.A modo de ejemplo, ¿cuál sería la regla que relaciona los números de la derecha con los de la izquierda en la siguiente lista?: 1 --------> 1 2 --------> 4 3 --------> 9 4 --------> 16x -------> x2.La regla es entonces "elevar al cuadrado":Para referirse a esta regla podemos usar un nombre, que por lo generales la letra f (de función). f es la regla "elevar al cuadrado el número".Usualmente se emplean dos notaciones:x --------> x2 ó f(x) = x2 .Así, f(3) significa aplicar la regla f a 3. Al hacerlo resulta 32 = 9.Entonces f(3) = 9. De igual modo f(2) = 4, f(4) = 16 f(a) = a2, etc.
Definición formal:
Una función f es una regla que asigna a cada elemento x de un conjunto X exactamente un elemento, llamado f(x) de un conjunto Y. Otra definición equivalente es: sean X e Y dos conjuntos. Una función de X en Yen X.
observa con atención el siguiente video. Aquí aclaras la diferencia entre relación y función
ECUACIONES CON VALOR ABSOLUTO
El valor absoluto o numérico de un número es la distancia del mismo con respecto al 0 en la recta numérica.
El valor absoluto de cualquier número es siempre positivo.
Entonces | x | = x
| x | = -(-x ) = x si x ‹ 0
PROPIEDADES
* No Negatividad: Establece que el valor absoluto de un número nunca puede ser negativo.
* El producto de dos números es siempre igual al producto de los módulos de ambos números tomados por separado.
| xy| = | x | | y |
* suma de dos números es siempre igual a la suma por separado del módulo de ambos números.
| x + y| = | x | + | y |
En combinación con estas cuatro propiedades fundamentales, algunas otras de las propiedades más importantes son:
* Simetría: Establece que la definición básica del valor absoluto es, en otras palabras, ignorar el signo negativo.
| - x | = x
* La división de dos números es siempre igual a la división del módulo de los dos números por separado.
| x / y| = | x | / | y | si y 0
observa el siguiente video
INECUACIONES CON VALOR ABSOLUTO
Para resolver una inecuación con valor absoluto, se debe tener en cuenta las siguientes propiedades:
propiedades del valor absoluto
|x| = a son los valores x tales que x = a o x = - a
|x| < a son los valores x tales que - a < x < a
|x| > a son los valores x tales que x < - a o x > a
La desigualdad |x|≤a describe el intervalo cerrado [-a, a], simétrico respecto al origen.
Y los números reales |x| < a son los del intervalo abierto (-a, a).
La desigualdad |x| ≥ a describe la unión de los intervalos (-∞, -a]∪[a, ∞).
Y los números reales |x|> a son la unión de los intervalos abiertos (-∞, -a)∪(a, ∞).
La desigualdad |x - c| < d es el intervalo abierto (c-d, c+d), denominado también entorno de centro c y radio d, E(c , r).
La desigualdad |x - c|≤d es el intervalo cerrado [c -d , c+d].
La desigualdad |x - c|>d es la unión de los intervalos (-∞, c-d) ∪ (c+d, ∞).
La desigualdad |x-c|≥d es la unión de los intervalos (-∞, c-d] ∪ [c+d, ∞).
Ejemplos de las propiedades del valor absoluto
a) La expresión |x| < 5 representa el intervalo abierto (-5, 5)
|x| < 5 ⇔ -5 < x < 5 ⇔ x ∈ (-5,5)
b) La expresión |x| ≤ 5 representa el intervalo cerrado [-5, 5]
|x| ≤ 5 ⇔ -5 ≤ x ≤ 5 ⇔ x ∈ [-5,5]
c) La expresión |x-5| ≤ 7 representa el intervalo cerrado [-2, 12]
pues |x-5|≤7 ⇔ -7≤x-5≤7 ⇔ -7+5≤ x ≤ 7+5 ⇔ -2≤x≤12 ⇔ x∈[-2, 12]
d) La expresión |x| > 5 representa la unión de intervalos (-∞, -5)∪(5, ∞), pues
|x| > 5 ⇔ x < -5 o x > 5 ⇔ x ∈ (-∞ , -5) ∪ (5 , ∞)
e) La expresión |x-5|≥7 representa la unión de intervalos (-∞,-2]∪[12,∞), pues
|x-5| ≥ 7 ⇔ x-5 ≤ -7 o x-5 ≥ 7 ⇔ x ≤ 5-7 o x≥5+7 ⇔ x ∈ (-∞ , -2] ∪ [12 , ∞)
OBSERVA los siguientes videos para reforzar los conceptos y propiedades vistas anteriormente
Ecuaciones con valor absoluto
Inecuaciones con valor absoluto
DESIGUALDADES
Una desigualdad es una expresión matemática que contiene un signo de desigualdad. Los signos de desigualdad son:
≠ no es igual
< menor que
> mayor que
≤ menor o igual que
≥ mayor o igual que
De la definición de desigualdad, lo mismo que de la escala de los números algebraicos, se deducen algunas consecuencias, a saber:
1º Todo número positivo es mayor que cero
Ejemplo:
5 > 0 ; porque 5 – 0 = 5
2º Todo número negativo es menor que cero
Ejemplo:
–9 < 0 ; porque –9 –0 = –9
3º Si dos números son negativos, es mayor el que tiene menor valor absoluto ;
Ejemplo:
–10 > –30; porque -10 – (–30) = –10 +30 = 20
Una desigualdad que contiene al menos una variable se llama inecuación .
Por ejemplo:
X + 3 < 7
(La punta del signo < siempre señala el menor)
Ejemplos:
3 < 4, 4 > 3
¿Cómo resolvemos una inecuación? Para esto tenemos que conocer y entender las propiedades de las desigualdades.
Propiedades de las desigualdades
1. Una desigualdad no varía si se suma o resta la misma cantidad a ambos lados:
a < b / ± c (sumamos o restamos c a ambos lados)
a ± c < b ± c
Ejemplo:
2 + x > 16 / – 2 (restamos 2 a ambos lados)
2 + x − 2 > 16 − 2
x > 14
2. Una desigualdad no varía su sentido si se multiplica o divide por un número positivo:
a < b / • c (c > 0) (c es positivo, mayor que cero)
a • c < b • c
a > b / • c (c > 0) ( c es positivo, mayor que cero)
a • c > b • c
Ejemplo
3 ≤ 5 • x / :5
3/5 ≤ x esto es, todos los reales mayores o iguales que 3/5
3. Una desigualdad varía su sentido si se multiplica o divide por un número negativo:
a < b / • c (c < 0) (c es negativo, menor que cero)
a • c > b • c
a > b / • c (c < 0) ( c es negativo, menor que cero)
a • c < b • c
Ejemplo:
15 – 3 • x ≥ 39 / −15
− 3 • x ≥ 39 – 15 /: −3
x ≤ 24: (−3)
x ≤ − 8. Esto es, todos los reales menores o iguales que −8.
De manera recíproca, cuando la parte de la incógnita resulta negativa deben invertirse los signos a ambos lados y cambiar el sentido de la desigualdad, ya que no puede haber desigualdades con incógnita negativa.
El siguiente video te explica las anteriores propiedades . OBSERVA.
PROPIEDADES DE LAS INECUACIONES
1. Si a los dos miembros de una inecuación se les suma o se les resta un mismo número, la inecuación resultante es equivalente a la dada.
3x + 4 < 5
3x + 4 − 4 < 5 − 4
3x < 1
2. Si a los dos miembros de una inecuación se les multiplica o divide por un mismo número positivo, la inecuación resultante es equivalente a la dada.
2x : 2 < 6 : 2
x < 3
3. Si a los dos miembros de una inecuación se les multiplica o divide por un mismo número negativo, la inecuación resultante cambia de sentido y es equivalente a la dada.
−x < 5
3. Si a los dos miembros de una inecuación se les multiplica o divide por un mismo número negativo, la inecuación resultante cambia de sentido y es equivalente a la dada.
−x < 5
(−x) · (−1) > 5 · (−1)
x > −5
INECUACIONES DE PRIMER GRADO
La teoría de conjuntos es una rama de las matemáticas que estudia las propiedades y relaciones de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.
CONJUNTO
La palabra conjunto generalmente la asociamos con la idea de agrupar objetos, por ejemplo un conjunto de discos, de libros, de plantas de cultivo y en otras ocasiones en palabras como hato, rebaño, piara, parcelas, campesinado, familia, etc., es decir la palabra conjunto denota una colección de elementos claramente entre sí, que guardan alguna característica en común. Ya sean números, personas, figuras, ideas y conceptos.
En matemáticas el concepto de conjunto es considerado primitivo y ni se da una definición de este, sino que se trabaja con la notación de colección y agrupamiento de objetos, lo mismo puede decirse que se consideren primitivas las ideas de elemento y pertenencia.
La característica esencial de un conjunto es la de estar bien definido, es decir que dado un objeto particular, determinar si este pertenece o no al conjunto. Por ejemplo si se considera el conjunto de los números dígitos, sabemos que el 3 pertenece al conjunto, pero el 19 no. Por otro lado el conjunto de las bellas obras musicales no es un conjunto bien definido, puesto que diferentes personas puedan incluir distintas obras en el conjunto.
Los objetos que forman un conjunto son llamados miembros o elementos. Por ejemplo el conjunto de las letras de alfabeto; a, b, c, ..., x, y, z. que se puede escribir así:
{ a, b, c, ..., x, y, z}
Como se muestra el conjunto se escribe entre llaves ({}) , o separados por comas (,).
El detallar a todos los elementos de un conjunto entre las llaves, se denomina forma tabular, extensión o enumeración de los elementos.
Dos conjuntos son iguales si tienen los mismos elementos, por ejemplo:
El conjunto { a, b, c } también puede escribirse:
{ a, c, b }, { b, a, c }, { b, c, a }, { c, a, b }, { c, b, a }
En teoría de conjuntos se acostumbra no repetir a los elementos por ejemplo:
El conjunto { b, b, b, d, d } simplemente será { b, d }.
Los conjuntos se denotan por letras mayúsculas : A, B, C,... por ejemplo:
A={ a, c, b }
B={ primavera, verano, otoño, invierno }
El símbolo Î indicará que un elemento pertenece o es miembro de un conjunto. Por el contrario para indicar que un elemento no pertenece al conjunto de referencia, bastará cancelarlo con una raya inclinada / quedando el símbolo como Ï .
Ejemplo:
Sea B={ a, e, i, o, u }, a Î B y c Ï B
SUBCONJUNTO
Sean los conjuntos A={ 0, 1, 2, 3, 5, 8 } y B={ 1, 2, 5 }
En este caso decimos que B esta contenido en A, o que B es subconjunto de A. En general si A y B son dos conjuntos cualesquiera, decimos que B es un subconjunto de A si todo elemento de B lo es de A también.
Por lo tanto si B es un subconjunto de A se escribe B Ì A. Si B no es subconjunto de A se indicará con una diagonal Ë .
Note que Î se utiliza solo para elementos de un conjunto y Ì solo para conjuntos.
El conjunto que contiene a todos los elementos a los que se hace referencia recibe el nombre de conjunto Universal, este conjunto depende del problema que se estudia, se denota con la letra U y algunas veces con la letra S (espacio muestral).
Por ejemplo si solo queremos referirnos a los 5 primeros números naturales el conjunto queda:
Forma alternativa para indicar conjuntos de gran importancia:
- Conjunto de números naturales (enteros mayores que cero) representados por la letra N donde
- Conjunto de números enteros positivos y negativos representados por la letra Z donde
- Conjunto de números racionales (números que se representan como el cociente de dos números enteros {fracciones }). Estos números se representan por una Q
- Conjunto de números irracionales (números que no puedan representarse como el cociente de dos números enteros) representados por la letra I.
- Conjunto de los números reales que son los números racionales e irracionales es decir todos, representados por R.
Todos estos conjuntos tienen un número infinito de elementos, la forma de simbolizarlos por extensión o por enumeración es de gran utilidad cuando los conjuntos a los que se hace referencia tienen pocos elementos para poder trabajar con ellos se emplean la notación llamada comprensión.
Por ejemplo, la denotar el conjunto de los números naturales menores que 60. Aquí U es el conjunto N y se tiene una propiedad que caracteriza a los elementos del conjunto: ser menores que 60.
Para indicar esta situación empleamos la simbología del álgebra de conjuntos:
En esta expresión se maneja un conjunto de x que pertenece a los números naturales (N) y además que los valores de x son menores que 60.
Ahora si se desea trabajar con conjuntos que manejen intervalos estos pueden ser representados por medio de una expresión algebraica; supongamos que se desea expresar los números enteros (Z) entre -20 y 30 el conjunto quedaría de la manera siguiente:
También se puede expresar el valor de un conjunto indicando la pertenencia o no pertenencia a uno diferente, por ejemplo
En el conjunto P se indica que los elementos x de un conjunto pertenecen a los números naturales y además x no pertenece al conjunto L.
OPERACIONES CON CONJUNTOS
UNIÓN
La unión de dos conjuntos A y B la denotaremos por A È B y es el conjunto formado por los elementos que pertenecen al menos a uno de ellos ó a los dos. Lo que se denota por:
A È B = { x/x Î A ó x Î B }
Ejemplo: Sean los conjuntos A={ 1, 3, 5, 7, 9 } y B={ 10, 11, 12 }
A È B ={ 1, 3, 5, 7, 9, 10, 11, 12 }
Ejemplo: Sean los conjuntos A={ a, b,c,d,e } y B={ a,e,i,o}
Ejemplo: Sean los conjuntos A={ a, b,c,d,e } y B={ a,e,i,o}
A È B ={ a, e, i ,o, b ,c, d }
La solución para AUB es lo sombreado de color verde.
A U B
La solución para AUB es lo sombreado de color verde.
A U B
INTERSECCIÓN
Sean A={ 1, 2, 3, 4, 5, 6, 8, 9 } y B={ 2, 4, 8, 12 }
Los elementos comunes a los dos conjuntos son: { 2, 4, 8 }. A este conjunto se le llama intersección de A y B; y se denota por A Ç B, algebraicamente se escribe así:
A Ç B = { x/x Î A y x Î B }
Y se lee el conjunto de elementos x que están en A y están en B.
La solución para AÇB es lo sombreado de color verde.
La solución para AÇB es lo sombreado de color verde.
Ejemplo:
Sean Q={ a, n, p, y, q, s, r, o, b, k } y P={ l, u, a, o, s, r, b, v, y, z }
Q Ç P={ a, b, o, r, s, y }
CONJUNTO VACÍO
Un conjunto que no tiene elementos es llamado conjunto vacío ó conjunto nulo lo que denotamos por el símbolo Æ .
Por ejemplo:
Sean A={ 2, 4, 6 } y B={ 1, 3, 5, 7 } encontrar A Ç B.
A Ç B= { }
El resultado de A Ç B= { } muestra que no hay elementos entre las llaves, si este es el caso se le llamará conjunto vacío ó nulo y se puede representar como:
A Ç B=Æ
CONJUNTOS AJENOS
Sí la intersección de dos conjuntos es igual al conjunto vacío, entonces a estos conjuntos les llamaremos conjuntos ajenos, es decir:
Si A Ç B = Æ entonces A y B son ajenos.
COMPLEMENTO
El complemento de un conjunto respecto al universo U es el conjunto de elementos de U que no pertenecen a A y se denota como A' o también y que se representa por comprehensión como:
A'={ x Î U/x y x Ï A }
Ejemplo:
Sea U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }
A= { 1, 3, 5, 7, 9 } donde A Ì U
El complemento de A estará dado por:
A'= { 2, 4, 6, 8 }
DIFERENCIA
Sean A y B dos conjuntos. La diferencia de A y B se denota por A-B y es el conjunto de los elementos de A que no están en B y se representa por comprehensión como:
A - B={ x/x Î A ; X Ï B }
Ejemplo:
Sea A= { a, b, c, d } y
B= { a, b, c, g, h, i }
A - B= { d }
En el ejemplo anterior se observa que solo interesan los elementos del conjunto A que no estén en B. Si la operación fuera B - A el resultado es
B – A = { g, h, i }
E indica los elementos que están en B y no en A.
DIAGRAMAS DE VENN
Los diagramas de Venn que de deben al filósofo inglés John Venn (1834-1883) sirven para encontrar relaciones entre conjuntos de manera gráfica mediante dibujos ó diagramas.
La manera de representar el conjunto Universal es un rectángulo, ó bien la hoja de papel con que se trabaje.
Un ejemplo de la representación del conjunto universal se muestra como:
Tautologías, Contradicción y Contingencia.
♦Con cinco conectivas lógicas básicas se construyen proposiciones compuestas que pueden ser tautologías, contradicciones o contingencias.
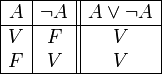
Si la tabla de verdad de la proposición es siempre verdadera, independientemente de la verdad o falsedad de las proposiciones simples, entonces la expresión es tautológica.
- Si la tabla de verdad es siempre falsa, será una contradicción.
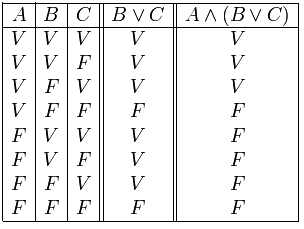
Si es verdadera y falsa, la proposición es una contingencia.
•TAUTOLOGÍA: Una proposición compuesta es una tautología si es verdadera para todas las asignaciones de valores de verdad para sus proposiciones componentes. Dicho de otra forma, su valor V no depende de los valores de verdad de las proposiciones que la forman, sino de la forma en que están establecidas las relaciones sintácticas de unas con otras. Sea el caso: 
•CONTRADICCIÓN: Se entiende por proposición contradictoria, o contradicción, aquella proposición que en todos los casos posibles de su tabla de verdad su valor siempre es F. Dicho de otra forma, su valor F no depende de los valores de verdad de las proposiciones que la forman, sino de la forma en que están establecidas las relaciones sintácticas de unas con otras. Sea el caso: 
•CONTINGENCIA:Se entiende por verdad contingente, o verdad de hecho, aquella proposición que puede ser verdadera o falsa, (combinación entre tautología y contradicción) según los valores de las proposiciones que la integran. Sea el caso: 
Cuantificadores.
El cuantificador universal: indica que algo es cierto para todos los individuos.
Sea A una expresión y sea x una variable. Si deseamos indicar que A es verdadero para todos los posibles valores de x, escribiremos (∀x) A.
(∀x) es cuantificador universal.
A es el ámbito (alcance) del cuantificador.
El símbolo ∀ se lee “para todo”.
Ejemplo:
Todo el mundo tiene buena suerte de vez en cuando.
B ≡ “tener buena suerte de vez en cuando”
B(x) ≡ “x tiene buena suerte de vez en cuando”
∀ xB(x) en el conjunto de los seres humanos.
Cuantificador Existencial: Sea A una expresión y x una variable. Si deseamos indicar que A es verdadero para al menos un valor de la variable x, escribiremos ∃ xA.
∃ se denomina cuantificador existencial, y A es el ámbito o alcance del cuantificador existencial.
Ejemplo:
Hay una persona que ha irrumpido en el aula con malos modales.
B ≡ “irrumpir en el aula con malos modales”
B(x) ≡ “x irrumpe en el aula con malos modales”
∃xB(x) en el conjunto de los seres humanos.
Concepto de Proposición.
La proposición es la expresión lingüística del razonamiento, que se caracteriza por ser verdadera o falsa empíricamente, sin ambigüedades.
•TIPOS DE PROPOSICIONES
Proposiciones Simples:
Son aquellas que no tienen oraciones componentes afectadas por negaciones (“no”) o términos de enlace como conjunciones (“y”), disyunciones (“o”) o implicaciones (“si . . . entonces”). Pueden aparecer términos de enlace en el sujeto o en el predicado, pero no entre oraciones.
Proposiciones Compuestas:
Una proposición será compuesta si no es simple. Es decir, si está afectada por negaciones o términos de enlace entre oraciones componentes.
EJEMPLOS:
Simples:
•La ballena es roja.
•La raíz cuadrada de 16 es 4.
•Gustavo es alto.
•Teresa va a la escuela.
Compuestas:
•La ballena no es roja.
•Gustavo no es alto.
•Teresa va a la escuela o María es inteligente.
•4 es menor que 8 o 6 es mayor que 10.
•El 1 es el primer número primo y es mayor que cero.
•El 7 es mayor que 5 y 7 es menor que 10.
•Si Yolanda es estudiosa entonces pasará el examen.
•Si corro rápido entonces llegaré temprano.
•Terminaré rápido si y sólo si me doy prisa.
•Aprenderé Matemáticas si y sólo si estudio mucho.
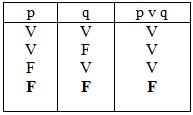
DISYUNCIÓN: Se representan dos enunciados separadas por la expresión o basta con que una sea verdadera para que se cumpla la proposición (pvq). Su símbolo es: V
EJEMPLOS:
Está lloviendo o es de noche.
Está feliz o está enojado.
Está caminando o está lloviendo.
Hay derivadas o hay integrales.
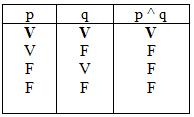
~CONJUNCIÓN: Es cuando dos proposiciones simples se combinan mediante la expresión y , la proposición compuesta resultante se le llama conjunción (pΛq). Su símbolo es: Λ, &, ·
EJEMPLOS:
La puerta está vieja y oxidada.
Hace frío y está nevando.
Está lloviendo y es de noche.
Tiene gasolina y tiene corriente.
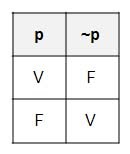
~NEGACIÓN: Si p es una proposición fundamental, de ésta se puede formar otra proposición, que se le llama Negación de p, escribiendo: “Es falso que” antes de p, ó, cuando es posible, se inserta en p la palabra “No”, (¬ p) Su símbolo es: ¬, ~
EJEMPLOS:
No está lloviendo.
La señora no ceno.
Es falso que 5×2=12.
Es falso que Alemania se encuentra en Europa.
~CONDICIONAL: Es aquella proposición compleja cuya conectiva dominante es el condicional, es decir, aquella expresión apofánatica que tiene la forma p → q, y que se lee “si p, entonces q” o bien “p es condición suficiente de q”, donde A es el antecedente y B el consecuente. Su símbolo es: →
EJEMPLOS:
Si está dormido entonces está soñando.
Si quiere comer entonces tiene hambre.
Si Londres está en Inglaterra entonces París está en Francia.
Si hay gasolina en mi tanque entonces mi automóvil funciona.
~BICONDICIONAL: También llamado equivalencia o implicación doble, es una proposición de la forma “P si y sólo si Q”, en la cual tanto P como Q son ambas ciertas o ambas falsas. También se dice que Q es una condición necesaria y suficiente para P,(p↔q). Su símbolo es: ↔, ≡
EJEMPLOS:
Esta completo si y solo si tienes todas las actividades.
Saldrás si y solo si acabaste tu tarea.
Está lloviendo si y solo si está nublado.
3+2=5 si y solo si 4+4=8
Tablas de Verdad.
Una conjunción de enunciados es verdadera cuando las dos proposiciones son verdaderas, en los demàs casos es falsa.
- Una conjunción de enunciados en donde no todos son verdaderos es falsa.
- Una conjunción de enunciados en donde no todos son verdaderos es falsa.
- Lo que equivale a decir que basta que uno de sus componentes sea falsa para que toda la proposición sea falsa y sólo será verdadera en el caso de que ambos componentes lo sean.
- Lo que equivale a decir que basta que uno de sus componentes sea falsa para que toda la proposición sea falsa y sólo será verdadera en el caso de que ambos componentes lo sean.
“El auto enciende cuando tiene gasolina en el tanque y tiene corriente la bateria”
(v) p: Tiene gasolina el tanque. ✓
(v) q: Tiene corriente la bateria. ✓
(v) r: El auto enciende. ✓
(v) p: Tiene gasolina el tanque. ✓
(f ) q: No tiene corriente la bateria. ✘
(f ) r: El auto no enciende. ✘
(f ) p: No tiene gasolina el tanque. ✘
(f ) q: No tiene corriente la bateria. ✘
(f ) r: El auto no enciende. ✘
•DISYUNCIÓN: La disyunción es verdadera, las dos proposiciones son falsas, en los demás casos es verdadero.
“Una persona puede entrar al cine si compra un boleto o si obtiene un pase”
(v) p: Compra un boleto. ✓
(v) q: Obtiene un pase. ✓
(v) r: Una persona entra al cine. ✓
(v) p: Compra un boleto. ✓
(f ) q: No obtiene un pase. ✘
(v) r: Una persona entra al cine. ✓
(f ) p: No compra un boleto. ✘
(f ) q: No obtiene un pase. ✘
(f ) r: Una persona no entra al cine. ✘
•CONDICIONAL: expresada por la frase “si,… entonces”, se simboliza mediante el signo “→” colocado entre las dos proposiciones.. La primera proposición lleva el nombre de antecedente y la segunda proposición la de consecuente.
La condicional será falsa sólo cuando el antecedente es verdadero y el consecuente es falso, en los demás caso será verdadera.
 “Si me saco la loteria entonces te regalaré un carro”
“Si me saco la loteria entonces te regalaré un carro”
(v) p:Si me saco la loteria. ✓
(v) q: Te regalaré un carro. ✓
(v) p→q: Si me saco la lotería entonces te regalaré un carro. ✓
(v) p:Si me saco la loteria. ✓
(f ) q: No te regalaré un carro. ✘
(f ) p→q: Si me saco la lotería entonces no te regalaré uncarro.✘⇩ ⇩ ⇩
(f ) p: Si no me saco la loteria. ✘
(f ) q: No te regalaré un carro. ✘
(f ) p→q: Si no me saco la lotería entonces no te regalaré un carro. ✓
•BICONDICIONAL: expresada por la frase “si y solo sí…”, denotada por el signo“↔”, significa una relación bidireccional en donde ambas proposiciones se necesitan entre sí.
La conectiva bicondicional será verdadera solamente si y solo si las dos sentencias que la componen son a la vez verdaderas o si son ambas falsas.
“La Tierra es esférica si y sólo si el Sol es una estrella”
(v) p: La Tierra es esférica. ✓
(v) q: El sol es una estrella. ✓
(v) p↔q: La Tierra es esférica si y sólo si el Sol es una estrella. ✓
“El Sol es una estrella si y solo si 1+2=4″
(v) p: El sol es una estrella. ✓
(f ) q: 1+2=4 ✘
(f ) p↔q: El Sol es una estrella si y solo si 1+2=4. ✘
“No serás un buen estudiante si y solo si no tienes promedio de 10″
(f ) p: No serás un buen estudiante. ✘
(f ) q: No tienes promedio de 10. ✘
(v ) p↔q:No serás un buen estudiante si y solo si no tienes promedio de 10. ✓
•NEGACIÓN: Dada una proposición simple p, esta puede ser negada y convertirse en otra proposición llamada negación de ~p. Este signo puede ser traducido en palabras, así: “no es el caso que” o, “es falso que” y más brevemente, “no”.
♦Se establece el siguiente principio para la negación lógica: La negación de un enunciado verdadero es falsa; la negación de un enunciado falso es verdadero.
(v) p: Está lloviendo. ✓
(f ) ~p: No está lloviendo. ✘
(f ) ~p: Es falso que Oscar habla por teléfono. ✘
(v) p: Oscar habla por teléfono. ✓
Definición de
EL CÁLCULO
La palabra cálculo proviene del término latino calculus (“piedra”) y se refiere a la cuenta, la enumeración o la pesquisa que se lleva a cabo mediante un ejercicio matemático. El concepto también se utiliza como sinónimo de conjetura.
El uso más extendido del término se encuentra en el ámbito de la lógica o de la matemática, donde el cálculo consiste en un algoritmo (un conjunto de instrucciones preestablecidas) que permite anticipar el resultado que procederá de ciertos datos que se conocen con anticipación. El origen etimológico de la palabra tiene que ver con las rocas que se empleaban en la antigüedad para realizar este tipo de cálculos.
Entre los distintos tipos de cálculos, podemos mencionar al cálculo algebraico (que emplea números y letras que aparecen en reemplazo de las cantidades) y al cálculo aritmético (que sólo utiliza números y ciertos signos que actúan por convención).
El uso más común del término "cálculo" es el lógico-matemático. Desde esta perspectiva, el cálculo consiste en un procedimiento mecánico, o algoritmo, mediante el cual podemos conocer las consecuencias que se derivan de unos datos previamente conocidos debidamente formalizados y simbolizados.
Ahora verás algunos videos que te aportan conocimiento sobre la historia del Cálculo, su definición y sus aplicaciones.
Lógica Proposicional.
Ejemplos:
Los unicos enteros positivos que dividen a 7 son 1 y el propio 7. (verdadero) ✓
Una decada tiene 10 años. (verdadera) ✓
La Tierra es plana. (falso) ✓
9 x 9 = 86. (falso) ✓
La Tierra es el unico planeta en el Universo que tiene vida. (puede ser verdadera o falsa, pero no ambas) ✘







































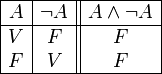


No hay comentarios:
Publicar un comentario