VOLUMEN DE LA PIRÁMIDE
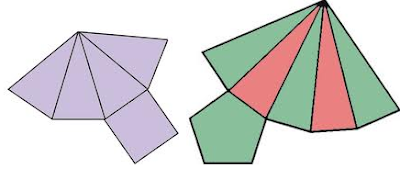
La pirámide es un poliedro, constituido por un polígono simple (llamado base) y sus caras laterales tienen forma de triángulos que tienen un único lado que coincide con uno del polígono base; todos los triángulos tienen un vértice común llamado vértice de la pirámide.
La altura que está desde el vértice de la pirámide y cae perpendicularmente a la base.
La base que es donde se apoya la pirámide
Las caras laterales que es cada uno de los triángulos que conforma su área lateral
La apotema que viene a ser la altura de cada triángulo.
La pirámide es un poliedro, constituido por un polígono simple (llamado base) y sus caras laterales tienen forma de triángulos que tienen un único lado que coincide con uno del polígono base; todos los triángulos tienen un vértice común llamado vértice de la pirámide.
Las pirámides toman el nombre de acuerdo al número de lados que tenga su base. Ejemplo: pirámide triangular, pirámide cuadrangular, pirámide pentagonal, etc.
En la figura anterior se tiene una pirámide pentagonal porque su base tiene cinco lados.
La pirámide tiene elementos como:
La base que es donde se apoya la pirámide
Las caras laterales que es cada uno de los triángulos que conforma su área lateral
La apotema que viene a ser la altura de cada triángulo.
CLASES DE PIRÁMIDES
Las pirámides se dividen según la forma del polígono de su base, según el ángulo que forma la base con su altura.
Imagen tomada de: http://webdelprofesor.ula.ve/nucleotrujillo/alperez/teoria/cap_01a-conceptos_geometricos/06a-solido-poliedro.htm
DESPLIEGUE DE PIRÁMIDES
Pirámide cuadrangular Pirámide Pentagonal
Pirámide cuadrangular Pirámide Pentagonal
ÁREA Y VOLUMEN DE LAS PIRÁMIDES
El área lateral se busca multiplicando el perímetro de la base por el apotema y dividiendo entre dos.
El área total es la suma del área lateral más el área de la base.
El volumen se busca multiplicando el área de la base por su altura y dividiendo entre 3.
Volumen, Área lateral y total de primas
El volumen de un prisma se halla multiplicando el área de la base por altura del cuerpo, es decir
V = Ab x H
Observa el siguiente video de aplicación
Ahora veamos el área lateral y área total de los prismas
Rectas paralelas cortadas por una secante
La relación entre dos rectas paralelas cortadas por una secante es un análisis clásico de la geometría euclidiana, que permite analizar una infinidad de problemas prácticos, así como definir algunos conceptos de interés en cuanto a congruencia y suplementaridad de ángulos.
Partiendo de dos rectas paralelas r y s, y una transversal t que corta a ambas, da lugar a ocho ángulos, cuya posición relativa da lugar a su definición.
Denominación de los ángulos
Ángulos adyacentes: Son los angulos que tienen un lado en común y sus otros dos lados son semirrectas opuestas.
Son ángulos adyacentes los siguientes pares de ángulos: a,b; c,d; a,c; b,d; e,f; g,h; e,g; f,h.
Los ángulos adyacentes son suplementarios, es decir, que la suman es 180°.
- Ángulos opuestos por el vértice: Si los lados de uno son semirrectas opuestas a los lados del otro.
Son ángulos opuestos por el vértice los siguientes pares de ángulos: a,d; b,c; e,h; f,g.
Los ángulos opuestos por el vértice son congruentes, es decir tienen la misma medida a cada lado del vértice.
- Ángulos alternos internos: Son los que se encuentran a distinto lado de la secante y en la zona interior de las rectas paralelas.
Son ángulos alternos internos los siguientes pares de ángulos: c,f; d,e.
Los ángulos alternos internos son congruentes.
- Ángulos alternos externos: Son los que se encuentran a distinto lado de la secante y en la zona externa de las rectas paralelas.
Son ángulos alternos externos los siguientes pares de ángulos: a,h; b,g.
Los ángulos alternos externos son congruentes.
- Ángulos colaterales internos: Son los que se encuentran del mismo lado de la secante y entre de las rectas.
Son ángulos colaterales internos los siguientes pares de ángulos: c,e; d,f.
Los ángulos colaterales internos son suplementarios.(suman 180°)
- Ángulos colaterales externos: Son los que se encuentran en uno y otro lado de la secante.
Son ángulos colaterales externos los siguientes pares de ángulos: a,g; b,h.
Los ángulos colaterales externos son suplementarios.(suman 180°)
- Ángulos correspondientes u homólogos: Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.
Son ángulos correspondientes los siguientes pares de ángulos: a,e; b,f; c,g; d,h.
Los ángulos correspondientes son congruentes.
LOS ÁNGULOS Y SU CLASIFICACIÓN
Con base en la teoría vista en nuestra clase de geometría, el siguiente video te sirve de refuerzo, para entender el concepto de los ángulos y como se clasifica:





No hay comentarios:
Publicar un comentario