OPERACIONES CON RADICALES
Con los radicales se pueden realizar las operaciones conocidas como la suma, resta, multiplicación y división.
Para poder sumar y restar radicales se requiere que los términos a operar sean semejantes, es decir que el radical tenga el mismo índice y la misma cantidad subradical, ejemplo:
video tomado de la dirección
https://www.youtube.com/watch?v=UCyLUpXmu-4
SUMA Y RESTA DE RADICALES
para sumar o restar radicales se debe realizar lo siguiente:
- se suman o restan los coeficientes de los radicales semejantes y se deja el mismo radical.
Ejemplos.
imagen tomada de la dirección http://www.videosdematematicas.com/algebra/sites/default/files/field/image/Suma%20y%20resta%20de%20radicales%20semejantes%20ejercicios%20resueltos.jpg
si a simple vista los radicales dados no son semejantes, tendremos que simplificar los radicales hasta donde sea posible y finalmente sumar los radicales simplificados que sean semejantes.
veamos algunos ejemplos en el siguiente video
este video fue tomado de la dirección https://www.youtube.com/watch?v=U_h7sXRZnp0
https://www.youtube.com/watch?v=EokPJbU57ww
Con los radicales se pueden realizar las operaciones conocidas como la suma, resta, multiplicación y división.
Para poder sumar y restar radicales se requiere que los términos a operar sean semejantes, es decir que el radical tenga el mismo índice y la misma cantidad subradical, ejemplo:
video tomado de la dirección
https://www.youtube.com/watch?v=UCyLUpXmu-4
SUMA Y RESTA DE RADICALES
para sumar o restar radicales se debe realizar lo siguiente:
- se suman o restan los coeficientes de los radicales semejantes y se deja el mismo radical.
Ejemplos.
imagen tomada de la dirección http://www.videosdematematicas.com/algebra/sites/default/files/field/image/Suma%20y%20resta%20de%20radicales%20semejantes%20ejercicios%20resueltos.jpg
si a simple vista los radicales dados no son semejantes, tendremos que simplificar los radicales hasta donde sea posible y finalmente sumar los radicales simplificados que sean semejantes.
veamos algunos ejemplos en el siguiente video
este video fue tomado de la dirección https://www.youtube.com/watch?v=U_h7sXRZnp0
https://www.youtube.com/watch?v=EokPJbU57ww
FRACCIONES COMPLEJAS ALGEBRAICAS
Fracciones complejas algebraicas:
Una fracción compleja es aquella cuyo numerador o denominador ( o ambos ) esta conformado por otras fracciones.
Ejemplos:
Pasos para simplificar fracciones complejas:
- Resolver completamente las operaciones presentes en el numerador y denominador de la fracción compleja.
- Convertir una fracción compleja en una fracción simple.
3. Se simplifica al máximo la fracción algebraica resultante.
Aquí vamos a ver dos ejemplos de fracciones complejas:
1._
1. Lo primero que vamos hacer es ponerle un denominador al (1).
2. Aquí utilizamos el método de la carita feliz porque multiplicamos cruzados y los dos denominadores
.
3. Después que obtenemos el resultado con este método procedemos a multiplicar con el método de la oreja que es medios con medios y extremos con extremos
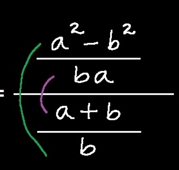
4. Después que tenemos la fracción de multiplicación del numerador y denominador que es esta etapa y la hacemos una fracción simple: como lo vamos aquí:
 5. En este paso ya pasamos a simplificar los terminos iguales y nos queda así como es una diferencia de cuadrados perfectos.
5. En este paso ya pasamos a simplificar los terminos iguales y nos queda así como es una diferencia de cuadrados perfectos.
6. Luego pasamos hacer este procedimiento que es la suma por la diferencia de cuadrados que es el resultado del numerador y en el denominador sigue igual el producto. como lo vemos aquí
7. Observamos que aquí hay factor común en el numerador y denominador, en lo cual pasamos a simplificar.
8. Bueno ya simplificado queda la respuesta planteada así.
2._ Este es el segundo ejemplo de fracción compleja:
*** Aquí va el numerador
1. Este es un ejercicio diferente al anterior ya que lo vamos a resolver por separado, primero resolvemos el numerador luego el denominador y cuando tengamos ambos resultados entonces construimos la fracción compleja, ya con una sola fracción arriba y abajo para convertirla en una fracción simple.
2. Comencemos con el numerador donde tenemos una suma de fracciones algebraicas heterogéneas, en el cual el MCD es el producto de los denominadores
3. Aquí procedemos a multiplicar con el método de la carita feliz que es en forma de (x).
4. Y sale esta respuesta ya multiplicada y luego pasamos desarrollar el numerador en el cual aplicamos la propiedad distributiva multiplicando lo de afuera con lo que esta dentro del paréntesis así y el denominador pasa con el mismo producto indicado:
6. En el siguiente paso ya aplicada la función distributiva queda otra respuesta como lo vemos a continuación así:
7. En este paso, pasamos a reducir terminos semejante como lo mostramos con las flechas de colores, y aquí va la respuesta de la reducción de terminos y ademas es el resultado del numerador.
*** Ahora pasamos al denominador
1. Aquí tenemos una resta de fracciones algebraicas
2. El (MCD) es el producto de estas dos expresiones del denominador que son: (x-2)(x+6) : y lo pasamos a realizar con el método de la carita feliz así:
3. Y aquí ya tenemos ensamblada la operación de la carita feliz: 4. Y así mismo aplicamos la propiedad distributiva como lo mostramos con las flechas de colores y el denominador pasa con el producto indicado:
4. Ahora vamos hacer la reducción de terminos semejantes en el numerador y lo mostramos con los colores en el numerador y queda la operación así:
5. Y esta es la respuesta del denominador. Luego todo pasa así desde el comienzo ya con el numerador y denominador ya resueltos para pasar hacer la fracción así:
*** Esta es la fracción con los resultados del numerador y del denominador con una sola fracción arriba y abajo:
6. Cambiamos esto en una fracción simple simplificando el numerador con el denominador ya que son iguales y el orden de los factores no alteran el producto:
7. Y nos queda así esta es la respuesta del ejercicio, en el numerador y en el denominador, esto no es posible simplificar a pesar que en el numerador podemos extraer el factor común de 8 pero eso no hace que se simplifique la fracción y termina así.
OBSERVA LA EXPLICACIÓN DE LOS SIGUIENTES EJERCICIOS
EJEMPLO 1.
EJEMPLO 2.
EJEMPLO 3
EJEMPLO 4.
OPERACIONES CON POLINOMIOS
Fracciones complejas algebraicas:
Una fracción compleja es aquella cuyo numerador o denominador ( o ambos ) esta conformado por otras fracciones.
Ejemplos:
Pasos para simplificar fracciones complejas:
- Resolver completamente las operaciones presentes en el numerador y denominador de la fracción compleja.
- Convertir una fracción compleja en una fracción simple.
3. Se simplifica al máximo la fracción algebraica resultante.
Aquí vamos a ver dos ejemplos de fracciones complejas:
1._
1. Lo primero que vamos hacer es ponerle un denominador al (1).
2. Aquí utilizamos el método de la carita feliz porque multiplicamos cruzados y los dos denominadores
.
3. Después que obtenemos el resultado con este método procedemos a multiplicar con el método de la oreja que es medios con medios y extremos con extremos
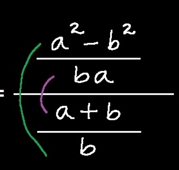
4. Después que tenemos la fracción de multiplicación del numerador y denominador que es esta etapa y la hacemos una fracción simple: como lo vamos aquí:
 5. En este paso ya pasamos a simplificar los terminos iguales y nos queda así como es una diferencia de cuadrados perfectos.
5. En este paso ya pasamos a simplificar los terminos iguales y nos queda así como es una diferencia de cuadrados perfectos.
6. Luego pasamos hacer este procedimiento que es la suma por la diferencia de cuadrados que es el resultado del numerador y en el denominador sigue igual el producto. como lo vemos aquí
7. Observamos que aquí hay factor común en el numerador y denominador, en lo cual pasamos a simplificar.
8. Bueno ya simplificado queda la respuesta planteada así.
2._ Este es el segundo ejemplo de fracción compleja:
*** Aquí va el numerador
1. Este es un ejercicio diferente al anterior ya que lo vamos a resolver por separado, primero resolvemos el numerador luego el denominador y cuando tengamos ambos resultados entonces construimos la fracción compleja, ya con una sola fracción arriba y abajo para convertirla en una fracción simple.
2. Comencemos con el numerador donde tenemos una suma de fracciones algebraicas heterogéneas, en el cual el MCD es el producto de los denominadores
3. Aquí procedemos a multiplicar con el método de la carita feliz que es en forma de (x).
4. Y sale esta respuesta ya multiplicada y luego pasamos desarrollar el numerador en el cual aplicamos la propiedad distributiva multiplicando lo de afuera con lo que esta dentro del paréntesis así y el denominador pasa con el mismo producto indicado:
6. En el siguiente paso ya aplicada la función distributiva queda otra respuesta como lo vemos a continuación así:
7. En este paso, pasamos a reducir terminos semejante como lo mostramos con las flechas de colores, y aquí va la respuesta de la reducción de terminos y ademas es el resultado del numerador.
*** Ahora pasamos al denominador
1. Aquí tenemos una resta de fracciones algebraicas
2. El (MCD) es el producto de estas dos expresiones del denominador que son: (x-2)(x+6) : y lo pasamos a realizar con el método de la carita feliz así:
3. Y aquí ya tenemos ensamblada la operación de la carita feliz: 4. Y así mismo aplicamos la propiedad distributiva como lo mostramos con las flechas de colores y el denominador pasa con el producto indicado:
4. Ahora vamos hacer la reducción de terminos semejantes en el numerador y lo mostramos con los colores en el numerador y queda la operación así:
5. Y esta es la respuesta del denominador. Luego todo pasa así desde el comienzo ya con el numerador y denominador ya resueltos para pasar hacer la fracción así:
*** Esta es la fracción con los resultados del numerador y del denominador con una sola fracción arriba y abajo:
6. Cambiamos esto en una fracción simple simplificando el numerador con el denominador ya que son iguales y el orden de los factores no alteran el producto:
7. Y nos queda así esta es la respuesta del ejercicio, en el numerador y en el denominador, esto no es posible simplificar a pesar que en el numerador podemos extraer el factor común de 8 pero eso no hace que se simplifique la fracción y termina así.
OBSERVA LA EXPLICACIÓN DE LOS SIGUIENTES EJERCICIOS
EJEMPLO 1.
EJEMPLO 2.
EJEMPLO 3
EJEMPLO 4.
OPERACIONES CON POLINOMIOS
Suma de polinomios
Para sumar dos polinomios se suman los coeficientes de los términos del mismo grado.
P(x) = 2x3 + 5x − 3
Q(x) = 4x − 3x2 + 2x3
1.Ordenamos los polinomios, si no lo están.
Q(x) = 2x3 − 3x2 + 4x
P(x)+Q(x)=(2x3+5x−3)+(2x3−3x2+4x)
2.Agrupamos los monomios del mismo grado.
P(x)+ Q(x) = 2x3 + 2x3 − 3x2 +5x +4x −3
3.Sumamos los monomios semejantes.
P(x) + Q(x) = 4x3− 3x2 +9x − 3
P(x) = 2x3 + 5x − 3
Q(x) = 4x − 3x2 + 2x3
1.Ordenamos los polinomios, si no lo están.
Q(x) = 2x3 − 3x2 + 4x
P(x)+Q(x)=(2x3+5x−3)+(2x3−3x2+4x)
2.Agrupamos los monomios del mismo grado.
P(x)+ Q(x) = 2x3 + 2x3 − 3x2 +5x +4x −3
3.Sumamos los monomios semejantes.
P(x) + Q(x) = 4x3− 3x2 +9x − 3
Observa los siguientes videos
Resta de polinomios
La resta de polinomios consiste en sumar al minuendo el opuesto del sustraendo.
P(x) − Q(x) = (2x3 +5x −3) −(2x3 − 3x2 + 4x)
P(x) − Q(x) = 2x3 +5x − 3 −2x3 + 3x2 −4x
P(x) − Q(x) = 2x3 −2x3 +3x2 + 5x−4x −3
P(x) − Q(x) = 3x2 +x −3
observa el siguiente video.
P(x) − Q(x) = (2x3 +5x −3) −(2x3 − 3x2 + 4x)
P(x) − Q(x) = 2x3 +5x − 3 −2x3 + 3x2 −4x
P(x) − Q(x) = 2x3 −2x3 +3x2 + 5x−4x −3
P(x) − Q(x) = 3x2 +x −3
Multiplicación de polinomios
Multiplicación de un número por un polinomio
Es otro polinomio que tiene de grado el mismo del polinomio y como coeficientes el producto de los coeficientes del polinomio por el número.
3(2x3 −3 x2 +4x −2)=6x3 −9x2 +12x −6
Observa el siguiente video
Observa el siguiente video
Multiplicación de un monomio por un polinomio.
Se multiplica el monomio por todos y cada uno de los monomios que forman el polinomio.
3x2 (2x3 −3x2 +4x −2)=6x5 −9x4 +12x3 −6x2
Observa el siguiente video
Multiplicación de polinomios
3x2 (2x3 −3x2 +4x −2)=6x5 −9x4 +12x3 −6x2
Observa el siguiente video
Multiplicación de polinomios
P(x) =2x2 −3 Q(x) =2x3 −3x2 +4x
Se multiplica cada monomio del primer polinomio por todos los elementos del segundo polinomio.
P(x) · Q(x) =(2x2 − 3)·(2x3 − 3x2 + 4x) =
= 4x5 −6x4 +8x3 −6x3 +9x2 −12x =
Se suman los monomios del mismo grado.
= 4x5 −6x4 +2x3 +9x2 −12
Se obtiene otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.
Esta forma de multiplicar polinomios es llamada multiplicación en línea o multiplicación horizontal.
Otro método para multiplicar polinomios es usar multiplicación vertical similar a la multiplicación vertical que se aprendió con números regulares. Demostremos este método con el mismo ejemplo.
Multiplicar cada término de arriba por x→
2x + 1
x + 3
________________
6x + 3 Multiplicar cada término de arriba por 3
2x2 + x
_______________
2x2 + 7x + 3 ←Ordenar términos semejantes uno sobre el otro y sumarlos verticalmente.
Este método es típicamente fácil de usar a pesar que se lleva más espacio. Solo hay que asegurarse que los términos semejantes se escriben juntos en columnas verticales para que sean fáciles de combinar al final.
OBSERVA EL SIGUIENTE VIDEO
Otro ejemplo
División de polinomios
Otro ejemplo
División de polinomios
Resolver la división de polinomios:
P(x) = x5 + 2x3 − x − 8 Q(x) = x2 − 2x + 1
P(x) : Q(x)
A la izquierda situamos el dividendo. Si el polinomio no es completo dejamos huecos en los lugares que correspondan.
A la izquierda situamos el dividendo. Si el polinomio no es completo dejamos espacios en los lugares que correspondan.
A la derecha situamos el divisor dentro de una caja.
A la izquierda situamos el dividendo. Si el polinomio no es completo dejamos huecos en los lugares que correspondan.
A la izquierda situamos el dividendo. Si el polinomio no es completo dejamos espacios en los lugares que correspondan.
A la derecha situamos el divisor dentro de una caja.
Dividimos el primer monomio del dividendo entre el
primer monomio del divisor.
x5 : x2 = x3
Multiplicamos cada término del polinomio divisor por el
resultado anterior y lo restamos del polinomio dividendo:
Volvemos a dividir el primer monomio del dividendo entre el
primer monomio del divisor. Y el resultado lo multiplicamos por el
divisor y lo restamos al dividendo.
2x4 : x2 = 2 x2

Volvemos a hacer las mismas operaciones.
8x2 : x2 = 8

10x − 6 es el resto, porque su grado es menor que el del
divisor y por tanto no se puede continuar dividiendo.
x3+2x2 +5x+8 es el cociente.
DIVISIÓN SINTÉTICA
La división sintética se realiza para simplificar la división de un polinomio entre otro polinomio de la forma x – c, logrando una manera mas compacta y sencilla de realizar la división
observe el siguiente video
Dividimos el primer monomio del dividendo entre el
primer monomio del divisor.
x5 : x2 = x3
Multiplicamos cada término del polinomio divisor por el
resultado anterior y lo restamos del polinomio dividendo:
Volvemos a dividir el primer monomio del dividendo entre el
primer monomio del divisor. Y el resultado lo multiplicamos por el
divisor y lo restamos al dividendo.
2x4 : x2 = 2 x2

Volvemos a hacer las mismas operaciones.
8x2 : x2 = 8

10x − 6 es el resto, porque su grado es menor que el del
divisor y por tanto no se puede continuar dividiendo.
x3+2x2 +5x+8 es el cociente.
DIVISIÓN SINTÉTICA
La división sintética se realiza para simplificar la división de un polinomio entre otro polinomio de la forma x – c, logrando una manera mas compacta y sencilla de realizar la división
observe el siguiente video
OBSERVE OTRO EJEMPLO
Los pasos para realizar una división sintética son:
1. Se ordenan los coeficientes de los términos en un orden decreciente de potencias de x hasta llegar al exponente cero rellenando con coeficientes cero donde haga falta.
2. Se deja un espacio libre hacia abajo y se traza una línea horizontal.
3. Se baja el primer coeficiente de la izquierda debajo de la linea horizontal.
4. Se multiplica el coeficiente que se bajo por el divisor y el resultado lo escribimos debajo del segundo coeficiente del dividendo y se realiza la suma de los coeficientes.
5. Se repite este procedimiento hasta terminar con el último coeficiente del dividendo.
Al terminar, el ùltimo número obtenido se llama residuo y los anteriores coeficientes serán el polinomio cociente o resultado.
Para escribir el resultado, se escriben los coeficientes obtenidos con la variable disminiuda en un grado del polinomio inicial.
Ejemplo: Dividir con división sintética
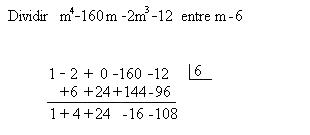
El residuo es -108.
Ejemplo:

EXPRESIONES ALGEBRAICAS
Una
expresión algebraica es una expresión matemática en la que se combinan números y letras.
8m + 2
Los números se denominan “coeficiente” y las letras “parte literal”.
La letra “a” representa una incógnita, es decir una variable de la que desconocemos su valor y que hay que calcular. El número que acompaña a la letra la va multiplicando.
3m = 3 x m
Por ejemplo:
Alberto tiene el doble de años que Carlos. ¿Qué edad tiene Alberto?
Edad de Alberto = 2a
La “a” representa la edad de Carlos; es una incógnita ya que por el momento desconocemos su valor.
El coeficiente 2 quiere decir que Alberto tiene el doble de edad que Carlos.
Si alguien nos dice la edad de Carlos, por ejemplo 7 años, sabremos el valor de la “a”.
a = 7 años
Luego ya podemos calcular la edad de Alberto.
Edad de Alberto = 2a = 2 x 7 = 14 años
La expresión algebraica puede tener varios sumandos. Cada sumando se denomina término.
3a + 5b + 3c – 7a
“3a” es un término, “5b” es otro término…
Cuando llego a conocer los valores de las letras (incógnitas) la expresión algebraica se transforma en una expresión numérica.
Por ejemplo, si en el ejemplo anterior el valor de las letras fuera:
a = 3
b = 2
c = 5
La expresión algebraica se transformaría:
3a + 5b + 3c – 7a = (3 x 3) + (5 x 2) + (3 x 5) – (7 x 3) = 13
A.- Monomios
Cuando una expresión algebraica tan sólo tiene un término se denomina monomio.
3b
Dos monomios que tienen la misma parte literal se dice que son semejantes:
Por ejemplo: En el jardín hay dos piedras, la primera pesa el doble que un ladrillo, y la segunda el triple.
Peso de la primera piedra: 2a
Peso de la segunda piedra: 3a
Ambos monomios, 2a y 3a, tiene la misma parte literal, la letra “a” (que representa el peso del ladrillo), luego ambos monomios son semejantes
El siguiente video te explica las expresiones algebraicas
OPERACIONES CON MONOMIOS
B.- Suma y resta de monomios
Si son monomios semejantes se mantiene la parte literal y se suman (restan) sus coeficientes:
3a + 4a = 7a
8a - 5a = 3a
Si los monomios no son semejantes no se pueden agrupar sus términos.
5a + 3b
9a – 8c
C.- Multiplicación y división de un monomio por un número
Se multiplica (o divide) el coeficiente por el número y se mantiene la parte literal.
4a x 2 = 8a
6a : 3 = 2a
OBSERVE OTRO EJEMPLO
Los pasos para realizar una división sintética son:
1. Se ordenan los coeficientes de los términos en un orden decreciente de potencias de x hasta llegar al exponente cero rellenando con coeficientes cero donde haga falta.
2. Se deja un espacio libre hacia abajo y se traza una línea horizontal.
3. Se baja el primer coeficiente de la izquierda debajo de la linea horizontal.
4. Se multiplica el coeficiente que se bajo por el divisor y el resultado lo escribimos debajo del segundo coeficiente del dividendo y se realiza la suma de los coeficientes.
5. Se repite este procedimiento hasta terminar con el último coeficiente del dividendo.
Al terminar, el ùltimo número obtenido se llama residuo y los anteriores coeficientes serán el polinomio cociente o resultado. Para escribir el resultado, se escriben los coeficientes obtenidos con la variable disminiuda en un grado del polinomio inicial.
Ejemplo: Dividir con división sintética
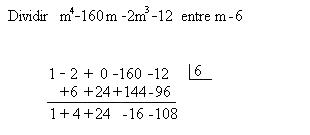
El residuo es -108.
Ejemplo:

EXPRESIONES ALGEBRAICAS
expresión algebraica es una expresión matemática en la que se combinan números y letras.
Los números se denominan “coeficiente” y las letras “parte literal”.
La letra “a” representa una incógnita, es decir una variable de la que desconocemos su valor y que hay que calcular. El número que acompaña a la letra la va multiplicando.
3m = 3 x m
Por ejemplo:
Alberto tiene el doble de años que Carlos. ¿Qué edad tiene Alberto?
Edad de Alberto = 2a
La “a” representa la edad de Carlos; es una incógnita ya que por el momento desconocemos su valor.
El coeficiente 2 quiere decir que Alberto tiene el doble de edad que Carlos.
Si alguien nos dice la edad de Carlos, por ejemplo 7 años, sabremos el valor de la “a”.
a = 7 años
Luego ya podemos calcular la edad de Alberto.
Edad de Alberto = 2a = 2 x 7 = 14 años
La expresión algebraica puede tener varios sumandos. Cada sumando se denomina término.
3a + 5b + 3c – 7a
“3a” es un término, “5b” es otro término…
Cuando llego a conocer los valores de las letras (incógnitas) la expresión algebraica se transforma en una expresión numérica.
Por ejemplo, si en el ejemplo anterior el valor de las letras fuera:
a = 3
b = 2
c = 5
La expresión algebraica se transformaría:
3a + 5b + 3c – 7a = (3 x 3) + (5 x 2) + (3 x 5) – (7 x 3) = 13
A.- Monomios
Cuando una expresión algebraica tan sólo tiene un término se denomina monomio.
3b
Dos monomios que tienen la misma parte literal se dice que son semejantes:
Por ejemplo: En el jardín hay dos piedras, la primera pesa el doble que un ladrillo, y la segunda el triple.
Peso de la primera piedra: 2a
Peso de la segunda piedra: 3a
Ambos monomios, 2a y 3a, tiene la misma parte literal, la letra “a” (que representa el peso del ladrillo), luego ambos monomios son semejantes
B.- Suma y resta de monomios
Si son monomios semejantes se mantiene la parte literal y se suman (restan) sus coeficientes:
3a + 4a = 7a
8a - 5a = 3a
Si los monomios no son semejantes no se pueden agrupar sus términos.
5a + 3b
9a – 8c
C.- Multiplicación y división de un monomio por un número
Se multiplica (o divide) el coeficiente por el número y se mantiene la parte literal.
4a x 2 = 8a
6a : 3 = 2a
Números irracionales
Un número irracional es un número que no se puede escribir en fracción - el decimal sigue para siempre sin repetirse.
Ejemplo: Pi es un número irracional. El valor de Pi es
3,1415926535897932384626433832795 (y más...)
Los decimales no siguen ningún patrón, y no se puede escribir ninguna fracción que tenga el valor Pi.
Números como 22/7 = 3,1428571428571... se acercan pero no son correctos.
| Se llama irracional porque no se puede escribir en forma de razón (o fracción), ¡no porque esté loco! |
Racional o irracional
Pero si un número se puede escribir en forma de fracción se le llama número racional:
Ejemplo: 9,5 se puede escribir en forma de fracción así
19/2 = 9,5
así que no es irracional (es un número racional)
Aquí tienes más ejemplos:
| Números | En fracción | ¿Racional o irracional? |
|---|---|---|
| 5 | 5/1 | Racional |
| 1,75 | 7/4 | Racional |
| .001 | 1/1000 | Racional |
| √2 (raíz cuadrada de 2) | ? | ¡Irracional! |
Ejemplo: ¿La raíz cuadrada de 2 es un número irracional?
Mi calculadora dice que la raíz de 2 es 1,4142135623730950488016887242097, ¡pero eso no es todo! De hecho sigue indefinidamente, sin que los números se repitan.
No se puede escribir una fracción que sea igual a la raíz de 2.Así que la raíz de 2 es un número irracional
Números irracionales famosos
 |
Pi es un número irracional famoso. Se han calculado más de un millón de cifras decimales y sigue sin repetirse. Los primeros son estos:
3,1415926535897932384626433832795 (y sigue...)
| ||||
 |
El número e (el número de Euler) es otro número irracional famoso. Se han calculado muchas cifras decimales de e sin encontrar ningún patrón. Los primeros decimales son:
2,7182818284590452353602874713527 (y sigue...)
| ||||
 |
La razón de oro es un número irracional. Sus primeros dígitos son:
1,61803398874989484820... (y más...)
| ||||
 |
Muchas raíces cuadradas, cúbicas, etc. también son irracionales. Ejemplos:
Pero √4 = 2, y √9 = 3, así que no todas las raíces son irracionales. |
GRÁFICA DE LOS NÚMEROS IRRACIONALES

Historia de los números irracionales
Aparentemente Hipaso (un estudiante de Pitágoras) descubrió los números irracionales intentando escribir la raíz de 2 en forma de fracción (se cree que usando geometría). Pero en su lugar demostró que no se puede escribir como fracción, así que es irracional.
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!
Ordenar números irracionales y representarlos en la recta numérica.
1- Recta numérica
Cuando trazamos una recta y a cada uno de sus puntos le asociamos un número, entonces tenemos una recta numérica. Todo número puede representarse en la recta.
1.1- Números irracionales en la recta numérica
A cada número racional le corresponde un punto en la recta pero en realidad éstos no completan la recta, también la constituyen los irracionales. En general, representar un número con infinitas cifras decimales no periódicas es imposible y por lo tanto nos tendríamos que conformar con una aproximación.
Sin embargo, con la ayuda del Teorema de pitágoras no es difícil representar geométricamente muchos números irracionales como √2, √3, √5, √6, √7, √8, √10,etc.
Para representarlo debemos seguir los siguientes pasos:
Paso 1: construir sobre la recta numérica un triángulo rectángulo de dimensiones 1cm de ancho 1cm de alto y vamos a llamar x a la hipotenusa.
Paso 2: aplicar el Teorema de Pitágoras como sigue:

Paso 3: Ya sabemos que el valor de la hipotenusa tiene como valor raíz de 2, luego con la ayuda de un compás podemos representar en la recta el valor de √2 de la siguiente manera. Con tu compás toma la dimensión de la hipotenusa, que en este caso es √2, y toma como centro el cero. Luego trazas un arco de circunferencia y el punto de corte con la recta numérica será el valor de raiz de 2 (longitud desde el punto cero al punto P).

Sabemos que √2 es un número irracional, por lo tanto, el punto P de la recta no puede estar ocupado por ningún otro número irracional.
En general, para localizar de manera geométrica √n, siendo n cualquier número natural, se puede aplicar el teorema de Pitágoras a un triángulo rectángulo de catetos 1 y la raíz cuadrada del número natural anterior, es decir, √n-1.
Por ejemplo, con el segmento de longitud √2 y un segmento de longitud 1, se construye un nuevo triángulo rectángulo. Se traza un arco de circunferencia centrada en el punto 0, y de radio igual a la hipotenusa de este nuevo triángulo. La intersección de este arco con la recta numérica es el punto √3 .
otra forma de representar una raiz es escribir el número que está dentro de la raíz, como la suma de dos números al cuadrado (por el Teorema de Pitágoras)
Por ejemplo:

Buscamos 2 numeros al cuadrado que sumados me den raíz de 3 y el único número al cuadrado que encuentro es la raíz de 2 y 1 al cuadrado. Estos dos números representan las medidas de los catetos del triángulo rectángulo.


1.2- Orden de las raíces cuadradas
Mientras mayor sea la cantidad subradical (numero que está bajo la raíz), mayor es la raíz.
√2 < √3 < √5 < √6 < √7
Por ejemplo: Ordena de menor a mayor las siguientes raíces:
√14; √5; √8; √3; √17.
Respuesta:
√3; √5; √8; √14; √17
LOS NÚMEROS REALES
El conjunto formado por los racionales e irracionales es elconjunto de los números reales, y su símbolo es la letra R.
Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo y la división por cero.
La recta real
La recta real
A todo número real le corresponde un punto de la recta y a todo punto de la recta un número real.
Los nùmeros reales pueden ser representados en la recta con tanta aproximación como queramos, pero hay casos en los que podemos representarlos de forma exacta.
Ahora veremos un poco de historia de los números reales con algunos videos. Debes estar atento a ellos para que contestes algunas preguntas sobre los videos 1 y 2.
video 1 LOS NUMEROS REALES
Video 2 Clasificación de los números Reales
Ahora debes contestar:
PREGUNTAS PARA EL Video 1
1. Sobre que animal se habla al comienzo del video y que experimento realizaron con él?
2.Que sistema numérico nos sirve para contar un determinado número de objetos?
3. Cuáles fueron las actividades humanas que crearon la necesidad de inventar los números enteros y racionales?
4. Por cuáles sistemas numéricos están compuestos los números reales?
5. Quien era Funes el Memorioso?
6. Que sucede si a un polígono regular se le aumentan el número de lados?
PREGUNTAS PARA EL Video 2
1. Realice un cuadro explicando cómo se clasifican los números reales.
2. Escriba cinco ejemplos para cada uno de los sistemas numéricos:
- números naturales
- números enteros
- números racionales
- números irracionales
En los nuímeros reales se pueden realizar operaciones con números naturales, enteros, racionales e irrracionales.
ahora veremos como se realizan las operaciones como la suma, resta, multiplicación y división de números racionales (fracciones),
SUMA Y RESTA
Las fracciones se clasifican en homogéneas (igual denominador) y hetereogéneas (diferente denominador). Veamos como se suman las homogéneas.
Con el mismo denominador. Se suman o se restan los numeradores y se mantiene el denominador.
Observa el video como ejemplo:
Con distinto denominador. En primer lugar se reducen los denominadores a común denominador, y se suman o se restan los numeradores de las fracciones equivalentes obtenidas.
Las fracciones también se pueden sumar o restar, realizando los productos en cruz, dividido entre el producto de los denominadores. Observa el siguiente video:
Ahora veamos las operaciones multiplicaciones y divisiones con fraccionarios.
MULTIPLICACION DE FRACCIONES
Para multiplicar fracciones se multiplican los numeradores entre si y los denominadores entre si. No importa si los denominadores son iguales o diferentes. Observa los siguientes ejemplos :
DIVISION DE FRACCIONES
Método 1. Multiplicar el cruz
Este método consiste en multiplicar el numerador de la primera fracción por el denominador de la segunda fracción y el resultado colocarlo en el numerador de la fracción final. Por otro lado, tenemos que multiplicar el denominador de la primera fracción por el numerador de la segunda fracción y el resultado lo escribimos en el denominador de la fracción final.
Se llama método de la cruz por el siguiente esquema:
En amarillo: Se multiplica el numerador de la primera por el denominador de la segunda. El resultado se escribe en el numerador.
En verde: Se multiplica el denominador de la primera por el numerador de la segunda. El resultado de escribe en el denominador.
Método 2: Invertir y multiplicar
Este método consiste en invertir la SEGUNDA FRACCIÓN, es decir, cambiar el denominador por el numerador y cambiar el numerador por el denominador. Después, se multiplican las dos fracciones.
Recuerda que para multiplicar fracciones se hace en línea: Numerador por numerador y denominador por denominador.
Siguiendo con el ejemplo anterior, tenemos que invertir la segunda fracción, por lo tanto cambiamos el 7 por el 5 y el 5 por el 7. Ahora cambiamos la división por una multiplicación.
Para multiplicar las dos fracciones tenemos que multiplicar el línea: numerador por numerador y denominador por denominador.
Como ves hemos obtenido el mismo resultado por lo dos métodos. ¿Cuál vas a utilizar tú?
observa el siguiente video para que refuerces el concepto.
























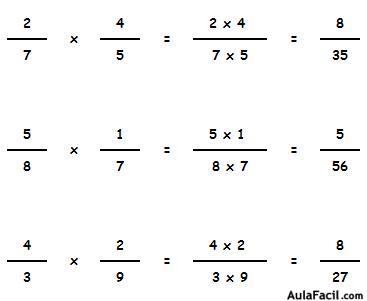




No hay comentarios:
Publicar un comentario