Taller de ecuaciones e inecuaciones de valor absoluto
Definición de valor absoluto
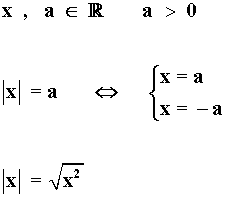
Ejemplos resueltos :
1. |3x| = 5
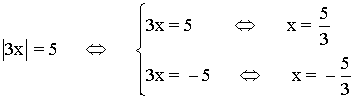
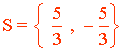
2. |x - 3| = 1
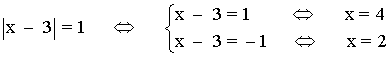
S = { 4 , 2 }
3.
|x + 4| = x + 1
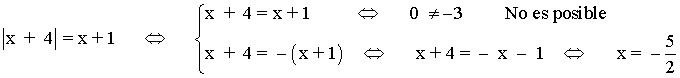
Comprobamos la solución:
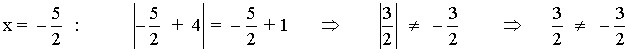
Por tanto, la ecuación no tiene solución.
Ejercicios:
Resuelve las siguientes ecuaciones con valor absoluto:
1) |x| = 4
2) |1 + 5x| = - 3
4) |x2 - 2| = 2 - 3x
5) |x + 1| = |x - 5l
Ejercicios:
Resuelve las siguientes inecuaciones de valor absoluto teniendo en cuenta las definiciones y los ejemplos resueltos.
|x| < a se expresa como:
- a < x < a
• |x| > a se expresa como:
x < - a ó x > a
• |x| ≤ a se expresa como:
- a ≤ x ≤ a
• |x| ≥ a se expresa como:
x ≤ - a ó x ≥ a
Ejercicios
Resuelve las siguientes inecuaciones:
1) |x| > 4
x < - 4 ó x > 4
x ∈ (-∞ , - 4) ∪ (4 , ∞)
2. |x| ≤ 4
- 4 ≤ x ≤ 4 ⇔ x ∈ [- 4 , 4]
3. |x - 3| > 1
x - 3 < - 1 ó x - 3 > 1
x - 3 < - 1 ⇔ x < - 1 + 3 ⇔ x < 2
x - 3 > 1 ⇔ x > 1 + 3 ⇔ x > 4
x ∈ (-∞ , 2) ∪ (4 , ∞)
4. |x - 1| ≤ 5x - 2
- (5x - 2) ≤ x - 1 ≤ 5x - 2
- 5x + 2 ≤ x - 1 ≤ 5x - 2
a) - 5x + 2 ≤ x - 1 ⇔ 2 + 1 ≤ x + 5x ⇔ 3 ≤ 6x ⇔ 1/2 ≤ x
b) x - 1 ≤ 5x - 2 ⇔ - 1 + 2 ≤ 5x - x ⇔ 1 ≤ 4x ⇔ 1/4 ≤ x
La solución será el conjunto de valores de x que cumplan a) y b), por tanto, es la intersección de los intervalos.
x ∈ [1/2 , ∞) ∩ [1/4 , ∞) = [1/2 , ∞)
Realiza las siguientes inecuaciones:
- 4 + |x| ≥ 3x
- |x2 - 1| < 3
-
TALLER DE INECUACIONES
A continuación están solucionados dos ejercicios; en el ejemplo 1 se resuelve una inecuación de primer grado, en el ejemplo 2, está resuelta una inecuación de segundo grado(cuadrática). Esto con el fin de reforzar el tema y tener un referente para que soluciones tu taller.
EJEMPLO 1. solucionar la inecuación 2( x + 1 ) - 3( x -2) < x+ 6
2( x + 1 ) - 3( x -2) < x + 6
2 x + 2 - 3x +6 < x + 6 (eliminacion de parèntesis)
2x - 3x -x < 6 - 6 - 2 ( las x a un lado y números al otro lado)
-2x < -2 (reducción tèrminos semejantes)
x >1 ( división a ambós lados por -2, cambio de sentido la desigualdad)
solución el intervalo ( 1 , + ¥)
EJEMPLO 2. solucionar la inecuaciòn x2 - 6x + 8 > 0
x2 - 6x + 8 > 0
(x - 4)× ( x - 2) > 0 (factorizando o tambíen aplicando la fórmula general)
(x - 4) < 0 y ( x - 2) < 0 o (x - 4) > 0 y ( x - 2) > 0
x < 4 y x < 2 o x > 4 y x > 2

S = (-∞, 2) U (4, ∞)
Ahora resuelve las siguientes inecuaciones con sus respectivas gráficas.
1. 2x + 1 £ x + 3
2. 3(2 - 5x)³ 18 - 12x
3.. x2 +3x − 4 < 0
4. 

5. 7x2 + 21x − 28 < 0
OBSERVA los siguientes vídeos, que te pueden servir para resolver sus ejercicios.
INECUACIONES
1)
Inecuaciones de primer grado
a) ( x - 2 )2 > (x + 2)×
( x - 2) + 8
|
R. ]
- ¥ , 0 [
|
b) ( x - 1 )2 <
x ( x - 4) + 8
|
R. ]
- ¥ , 7/2 [
|
c) 3 - ( x - 6) £ 4x - 5
|
R. [
14/5 , + ¥ [
|
d)
3x - 5 - x - 6 < 1
4 12
|
R. ]
- ¥ , 21/8 [
|
e) 1
- x - 5 < 9 + x
9
|
R. ]
-67/10 , + ¥ [
|
f) x
+ 6 - x + 6 £ x
.
3 15
|
R. [
120/11 , +¥ [
|
2)
Inecuaciones de segundo grado
a) x2
³ 16
|
R.
IR - ] -4 , 4[
|
b)
9x2 < 25
|
R.
] - 5/3 , 5/3 [
|
c) 36 > ( x - 1) 2
|
R.
] - 5 , 7 [
|
d)
(x + 5)2 £ ( x + 4 ) 2 + ( x - 3 )2
|
R.
IR - ] 0 , 8 [
|
e) x
( x - 2 ) < 2 ( x + 6)
|
R. ]
- 2 , 6 [
|
f) x2
- 3x > 3x - 9
|
R.
IR - í3ý
|
g) 4
( x - 1) > x2 + 9
|
R. Æ
|
h)
2x2 + 25 £
x ( x + 10 )
|
R. í5ý
|
i)
1 - 2x £ (x + 5)2 - 2(x +
1)
|
R.
IR
|
j)
3 > x ( 2x + 1)
|
R. ]
-3/2 , 1 [
|
k) x
( x + 1) ³ 15(1 - x2 )
|
R.
IR - ] -1 , 15/16 [
|
l) (
x - 2 ) 2 > 0
|
R.
IR - í2ý
|
m) (
x - 2)2 ³ 0
|
R.
IR
|
n) (
x - 2)2 < 0
|
R. Æ
|
o) (
x - 2)2 £
0
|
R. í2ý
|
3. Encuentra la región
solución de cada sistema.
y > x( x -3) 5x - 2
>-4
Taller de repaso
NÚMEROS ENTEROS Y RACIONALES
Este taller te refuerza conceptos que debes tener presentes para algunos temas del cálculo.
Los siguientes talleres están relacionados con el manejo de las proposiciones y teoría de conjuntos



No hay comentarios:
Publicar un comentario