taller ecuaciones e inecuaciones de valor absoluto

Taller de ecuaciones e inecuaciones de valor absoluto

Definición de valor absoluto

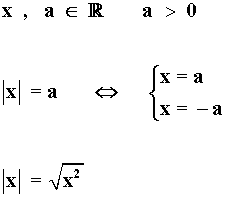
Ejemplos resueltos :

1. |3x| = 5

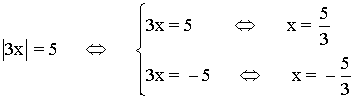
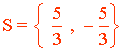
2. |x - 3| = 1

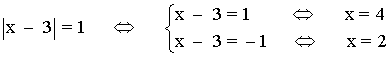
S = { 4 , 2 }

3.  

|x + 4| = x + 1

Comprobamos la solución:

Por tanto, la ecuación no tiene solución.

Ejercicios:

Resuelve las siguientes ecuaciones con valor absoluto:

1)   |x| = 4

2)    |1 + 5x| = - 3

4)   |x² - 2| = 2 - 3x

5)   |x + 1| = |x - 5l

Ejercicios:

    Resuelve las siguientes inecuaciones de valor absoluto teniendo en cuenta las definiciones y los ejemplos resueltos.

|x| < a  se expresa como:               

    - a < x  <  a

•   |x| > a  se expresa como:

                                                                     x < - a   ó  x > a

•   |x| ≤ a  se expresa como:               

    - a  ≤ x  ≤  a

•   |x| ≥ a  se expresa como:

                                                               x ≤ - a    ó   x ≥ a

Ejercicios  resueltos 

1) |x| > 4

x < - 4    ó    x > 4

x ∈ (-∞ , - 4) ∪ (4 , ∞)

2.  |x| ≤ 4

- 4 ≤ x ≤ 4     ⇔     x ∈ [- 4 , 4]

3.     |x - 3| > 1

x - 3 < - 1     ó     x - 3 > 1

x - 3 < - 1     ⇔     x < - 1 + 3     ⇔     x < 2

x - 3 > 1     ⇔     x > 1 + 3     ⇔     x > 4

x ∈ (-∞ , 2) ∪ (4 , ∞)

4.  |x - 1| ≤ 5x - 2

- (5x - 2)  ≤  x - 1  ≤  5x - 2

- 5x + 2  ≤  x - 1  ≤  5x - 2

a)   - 5x + 2 ≤ x - 1 ⇔  2 + 1 ≤ x + 5x  ⇔ 3 ≤ 6x     ⇔  1/2 ≤ x

b)   x - 1 ≤ 5x - 2     ⇔  - 1 + 2 ≤ 5x - x  ⇔  1 ≤ 4x     ⇔ 1/4 ≤ x

La solución será el conjunto de valores de x que cumplan a) y b), por tanto, es la intersección de los intervalos.

x ∈ [1/2 , ∞) ∩ [1/4 , ∞) = [1/2 , ∞)

Realiza las siguientes inecuaciones:

 1.  |x² - 1| < 3

          2.   |x + 1| ≥ 3

          3.    4 + |x| ≥ 3x