dominio y rango de una función

Funciones con radicales o funciones irracionales

Las funciones con radicales son las funciones que tienen la variable independiente   x   bajo el signo radical, es decir:

Las características generales de las funciones con radicales son:

1) Si   n   es un número par su dominio es el intervalo en el que   g(x) ≥ 0 .

2) Si   n   es impar, su dominio es R.

3) Su representación gráfica es una rama de una parábola.

1)   Ejemplo de función irracional:   f(x) = √x

1) Dominio:

Como   n   es par, el dominio de   f(x)   es el conjunto de valores donde   x ≥ 0 , es decir,   Dom(f) = [0, +∞)

2) Puntos de corte:

f(0) = √0 = 0  ,  es decir, el punto de corte coincide con el eje de coordenadas   (0, 0).

3) Tabla de valores:

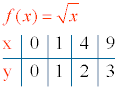
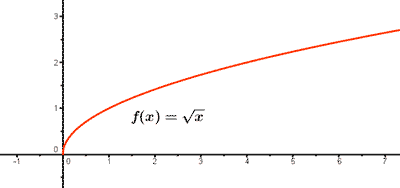
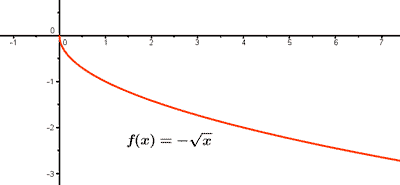
2)   Ejemplo de función irracional:   f(x) = - √x

1) Dominio:

Como   n   es par, el dominio de   f(x)   es el conjunto de valores donde   x ≥ 0 , es decir,   Dom(f) = [0, +∞)

2) Puntos de corte:

f(0) = - √0 = 0  ,  es decir, el punto de corte coincide con el eje de coordenadas   (0, 0).

3) Tabla de valores:

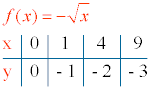
3)   Ejemplo de función irracional:   

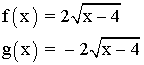
1) Dominio :

El dominio de  f (x)  y  g(x)  es el conjunto de valores donde  x - 4 ≥ 0,  es decir,  x ≥ 4.  Dom (f) = [ 4, + ∞ )   y   Dom (g) = [ 4, + ∞ ).

2) Puntos de corte :

x = 0  no pertenece al dominio de las funciones, por lo que no cortan al eje  y.



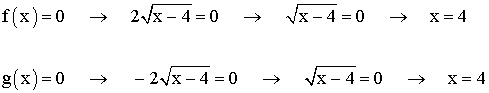
El punto de corte de ambas funciones con el eje  x  es el punto ( 4, 0 )

3)Tabla de valores :

f (x) : 

x	4	5	8	13
y	0	2	4	6

g (x) :

x	4	5	8	13
y	0	- 2	- 4	- 6

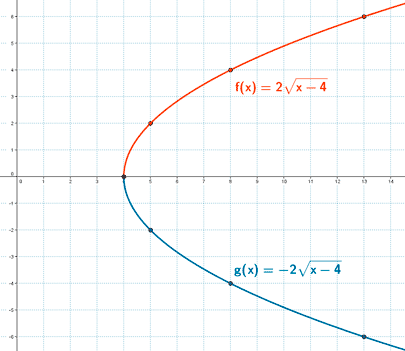
Ejemplo 4 :

1) Dominio :

El dominio de  f (x)  y de  g (x)  es el conjunto de valores donde  -x + 4 ≥ 0,  es decir,  - x ≥ -4   →   x ≤ 4.  Dom (f) = [ - ∞ , 4 ) y Dom (g) = [ - ∞ , 4 )

2) Puntos de corte :

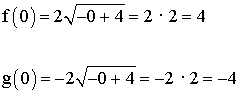
Punto de corte de f (x) con el eje  x :  ( 0, 4 ) y de g (x) con el eje x es el punto ( 0, - 4 



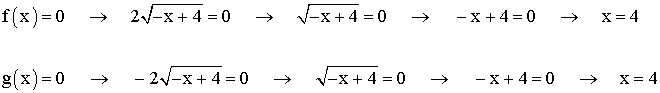
El punto de corte de ambas funciones con el eje  x  es el punto ( 4, 0 )

3)Tabla de valores :

f (x) : 

x	- 5	0	3	4
y	6	4	2	0

g (x) : 

x	- 5	0	3	4
y	- 6	- 4	- 2	0

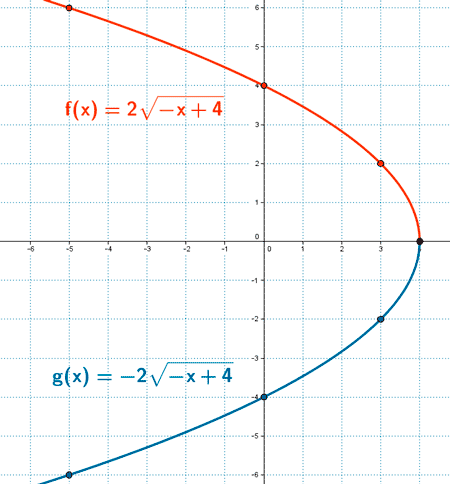
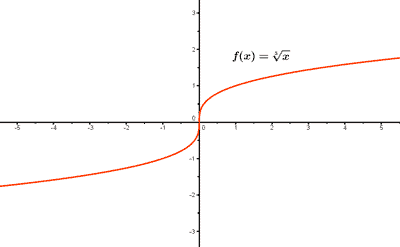
5)   Ejemplo de función irracional:   f(x) = ³√x

1) Dominio:

Como   n   es impar, el dominio de   f(x)   es el conjunto de todos los números reales , es decir,   Dom(f) = R .

2) Puntos de corte:

f(0) = ³√0 = 0  ,  es decir, el punto de corte coincide con el eje de coordenadas   (0, 0).

3) Tabla de valores:

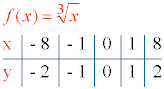
Dominio y Rango de una función 

Se dice que el dominio de una función son todos los valores que puede tomar el conjunto del dominio y que encuentra correspondencia en el conjunto llamado codominio, generalmente cuando se habla del plano, el dominio es el intervalo de valores que están sobre el eje de las X´s y que nos generan una asociación en el eje de las Y´s.

El otro conjunto que interviene en la definición es el conjunto llamado codominio o rango de la función, en ocasiones llamado imagen, este conjunto es la gama de valores que puede tomar la función; en el caso del plano son todos los valores que puede tomar la función  o valores en el eje de las Y´s.

También, cuando se grafica en el plano cartesiano se tiene una relación de dos variables, considerando como variable aquella literal que esta sujeta a los valores que puede tomar la otra.

VARIABLES DEPENDIENTES.
Son aquellas variables que como su nombre lo indica, dependen del valor que toma las otras variables Por ejemplo: f(x)= x, y o f(x) es la variable dependiente ya que esta sujeta a los valores que se le subministre a x. 
VARIABLE INDEPENDIENTE.
Es aquella variable que no depende de ninguna otra variable, en el ejemplo anterior la x es la variable independiente ya que la y es la que depende de los valores de x.
VARIABLE CONSTANTE.
Es aquella que no esta en función de ninguna variable y siempre tiene el mismo valor ejemplo:

Y=2, la constante gravitacional, entre otras.

observemos con los siguientes videos, sobre el dominio y rango de una función